As the Moon moves around the Earth, it has its orbit slightly inclined (about 5°) to the ecliptic, where the Earth moves around the Sun. Since the orbit of the Moon is slightly inclined, there exist two points where it crosses the ecliptic plane. These points are called lunar nodes. The ascending node is where the Moon crosses the ecliptic moving from South to North and the descending node is where the Moon crosses the ecliptic moving in the opposite direction from North to South. The Moon spends about half of its time below the ecliptic and half of its time above, usually crossing each node once a month (image courtesy of Wikipedia):
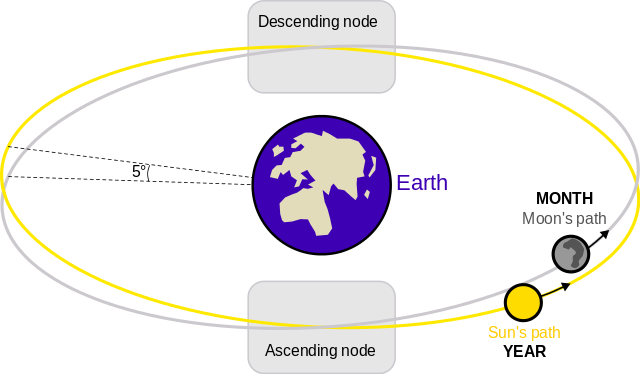
In Vedic astrology, the ascending node (also called the North node) is referred to as Rāhu and the descending node (also called the South node) is referred to as Ketu. Since the orbit of the Moon precesses in space, it crosses the ecliptic at slightly different points over time and this is seen as the movement of Rāhu and Ketu in the horoscope.
There are two ways the calculation of nodes can be approached: the true nodes and the mean nodes. The true nodes, as the name suggests, is where the orbit of the Moon actually crosses the ecliptic at the given time, assuming that the momentary orbit of the Moon is an adequate representation (see the section on true nodes in the Swiss Ephemeris documentation). The mean nodes are not the real crossing points, but are instead the approximation of the true nodes based on their average motion. Since mean nodes are based on average motion, if we try to calculate Rāhu and Ketu using mean nodes, we will observe that they always move in retrograde motion with a constant speed of 3’11” per day, which amounts to around 19°20’29” per year or a complete cycle of 360° in about 18.61296 years.
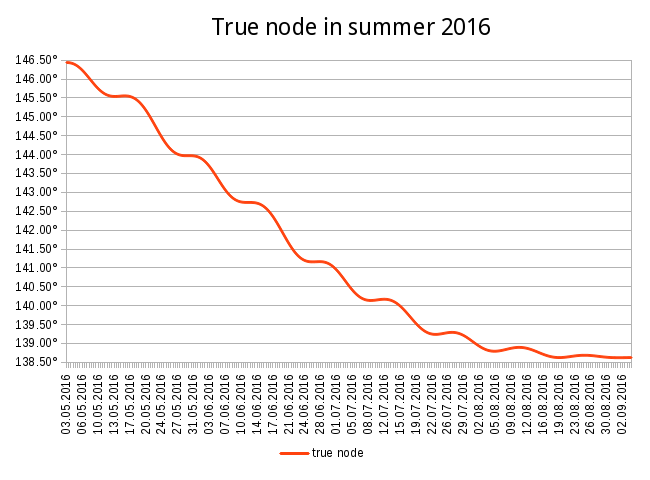
The true nodes, being the real crossing points, do not move in such a uniform fashion. Besides having a non-constant speed, it turns out that sometimes true nodes move in direct motion. In order to illustrate that, below is a table showing how the true North node (Rāhu) switches direction in the upcoming several months (the data for Ketu would be the same, except that it would be in the opposite Kumbha rāśi). It shows the direction of Rāhu’s motion, the date and time in UTC when this motion begins, Rāhu’s longitude at that time, and the distance it travels in that direction during the specified period:
| Motion | Date | Time | Degrees | Rāśi | Distance | Duration |
|---|---|---|---|---|---|---|
| retrograde | 03.05.2016 | 01:28 | 26°26’13” | Siṃha | -00°53’52” | 10 days 15:21 |
| direct | 13.05.2016 | 16:49 | 25°32’21” | Siṃha | 00°00’52” | 2 days 03:54 |
| retrograde | 15.05.2016 | 20:43 | 25°33’13” | Siṃha | -01°35’03” | 13 days 15:29 |
| direct | 29.05.2016 | 12:12 | 23°58’10” | Siṃha | 00°00’02” | 0 days 16:40 |
| retrograde | 30.05.2016 | 04:52 | 23°58’12” | Siṃha | -01°14’15” | 12 days 17:14 |
| direct | 11.06.2016 | 22:06 | 22°43’57” | Siṃha | 00°00’00” | 0 days 10:08 |
| retrograde | 12.06.2016 | 08:14 | 22°43’57” | Siṃha | -01°34’25” | 13 days 21:10 |
| direct | 26.06.2016 | 05:24 | 21°09’32” | Siṃha | 00°00’22” | 1 day 13:06 |
| retrograde | 27.06.2016 | 18:30 | 21°09’54” | Siṃha | -01°01’41” | 11 days 07:08 |
| direct | 09.07.2016 | 01:38 | 20°08’13” | Siṃha | 00°01’57” | 2 days 23:07 |
| retrograde | 12.07.2016 | 00:45 | 20°10’10” | Siṃha | -00°55’50” | 11 days 07:01 |
| direct | 23.07.2016 | 07:46 | 19°14’20” | Siṃha | 00°03’13” | 3 days 15:21 |
| retrograde | 26.07.2016 | 23:07 | 19°17’33” | Siṃha | -00°29’59” | 9 days 08:39 |
| direct | 05.08.2016 | 07:46 | 18°47’34” | Siṃha | 00°06’08” | 5 days 10:30 |
| retrograde | 10.08.2016 | 18:16 | 18°53’42” | Siṃha | -00°16’12” | 8 days 19:53 |
| direct | 19.08.2016 | 14:09 | 18°37’30” | Siṃha | 00°03’41” | 5 days 13:51 |
| retrograde | 25.08.2016 | 04:00 | 18°41’11” | Siṃha | -00°03’55” | 7 days 11:07 |
| direct | 01.09.2016 | 15:07 | 18°37’16” | Siṃha | 00°00’15” | 3 days 05:38 |
| retrograde | 04.09.2016 | 20:45 | 18°37’31” | Siṃha | -00°00’40” | 4 days 14:26 |
It can be seen in the table that the periods of direct motion are not that rare. In fact, the true node changes its direction several times per month. The distance it moves in direct motion is significantly less than in retrograde motion (the longest distance being 7’06” in VIII century), but it can stay in this motion for a noticeable period of time. The chart below depicts the data above in graphical format:
Here is another chart to compare the movement of the true node and the mean node based on the data for the current year:
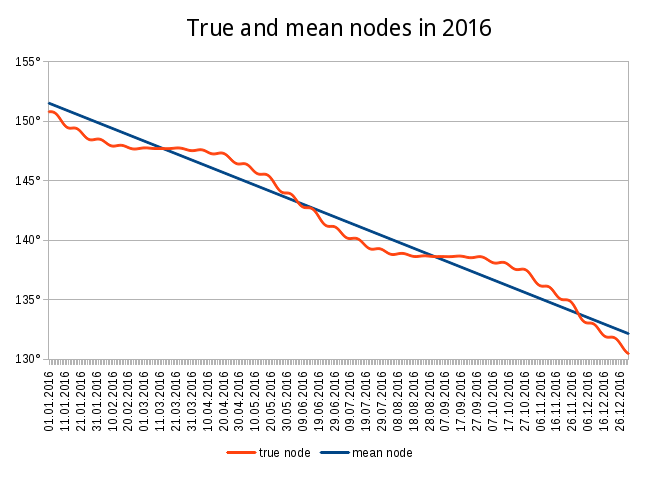
It can be seen on the graph that sometimes the true node is in front of the mean node and sometimes it is the other way round. The difference between the nodes can be as large as 2 degrees - in fact, it was as large as 2°00’04” in October 1458. In more recent years, it was 1°56’57” on November 12, 1959 and it will be 1°56’02” later this year on October 27, 2016.
Using mean nodes has the advantage for manual calculation using a node ephemeris. For instance, if we have the node’s longitude on one midnight and the next, we can calculate the precise longitude of the mean node for any time during the day using these two numbers alone. However, since mean nodes are based on average motion, there are times when the difference from the actual reality is quite significant. As an example, the Moon will cross the ecliptic going northward at 01:45 on October 26, 2016. The longitude of the Moon and the true North node (Rāhu) will coincide at 17°34’12” in Siṃha rāśi. However, the mean North node will be at 15°40’49”, which is 1°53’23” away from the crossing point. The longitude of the Moon and the mean North node will be the same at 15°41’18” several hours earlier at 22:06 on October 25, but the Moon will be 10’08” below the ecliptic.
The research effort above has helped us better understand the behavior of lunar nodes and make Chakra Darshana more efficient. We hope that it helps in your understanding of lunar nodes, too.
